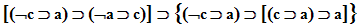Rhétorique de l’idéographie
Bruno Leclercq
Département de Philosophie, Université de Liège
Index
Mots-clés : démonstration, diagramme, image, mathématiques
Auteurs cités : Bernard Bolzano, Georg Cantor, Rudolf Carnap, Gottlob Frege, David Hilbert, Emmanuel KANT, Giuseppe Peano, Charles Sanders PEIRCE, Bertrand RUSSELL, Alfred Tarski, Alfred North Whitehead, Ludwig WITTGENSTEIN
- Note de bas de page 2 :
-
Emmanuel Kant, Critique de la raison pure, Paris, Gallimard, Folio Essais, A716/B744, p. 606.
- Note de bas de page 3 :
-
Emmanuel Kant, Critique de la raison pure, ibidem, B15, pp. 75-76.
Ce fut un trait majeur de la théorie de la démonstration des XIXème et XXème siècles que de s’être efforcée de minorer autant que possible, dans les preuves mathématiques, le rôle de l’intuition au profit de la seule déduction, et donc le rôle de la représentation visuelle des rapports mathématiques au profit de la seule représentation symbolique de leur dimension logique. Ainsi, alors que, dans sa Critique de la raison pure, Kant affirmait encore l’importance de s’appuyer sur l’image d’un triangle pour démontrer que la somme de ses angles est égale à deux droits2 ou sur l’image d’un alignement de points pour démontrer que 5+7=123, Bernard Bolzano insiste au contraire, dès 1810, sur le caractère purement analytique du jugement mathématique et sur la nature purement déductive de son raisonnement.
Déduction et intuition
- Note de bas de page 4 :
-
« Que la ligne droite soit entre deux points la plus courte, c’est une proposition synthétique. […] Le concept de plus court vient entièrement s’ajouter, et ne peut être tiré par aucune analyse du concept de la ligne droite. Il faut donc s’aider de l’intuition, au moyen de laquelle seulement la synthèse est possible » (Emmanuel Kant, Critique de la raison pure, ibidem, B15-B16, p. 76).
Pour Kant, les jugements mathématiques sont « synthétiques » – les propriétés attribuées au sujet ne sont pas déjà implicitement contenues en lui – et l’information nouvelle qu’ils contiennent ne peut dès lors être fournie que par une intuition4. Bien sûr, l’intuition dont il est ici question n’est pas simplement l’expérience sensible de cette ligne droite particulière qui est dessinée devant moi – expérience qui ne me renseigne que sur cette ligne droite particulière – mais bien l’intuition plus générale que ce qui vaut pour cette droite vaut aussi pour toutes les autres, intuition que Kant appelle « pure » parce qu’elle se reproduit à l’identique dans toute expérience même imaginaire de ligne droite et ne dépend donc pas des données sensibles singulières, sur lesquelles elle ne fait chaque fois que prendre appui.
Pour Bolzano, par contre, la connaissance mathématique est essentiellement conceptuelle et non intuitive. Si l’intuition de figures peut certes jouer un rôle psychologique d’adjuvant à la saisie de certains jugements mathématiques, elle ne constitue pas le fondement de leur validité, qui, par sa prétention à l’universalité mais aussi par son idéalité, dépasse forcément ce qui apparaît ici et maintenant dans telle ou telle intuition sensible :
- Note de bas de page 5 :
-
Bernard Bolzano, Contribution à une exposition mieux fondée des mathématiques, appendice traduit dans Philosophie, 1990, n° 27, § 9, p. 10.
« Je ne comprends pas du tout comment Kant a pu trouver, entre l’intuition qui fait voir un triangle dessiné réellement devant nous et celle qui fait voir un triangle simplement construit dans l’imagination, une différence si grande qu’il déclara la première superflue et insuffisante, la seconde au contraire nécessaire et suffisante, pour la preuve d’une proposition synthétique a priori. Selon ma conception, il est assurément inévitable que notre imagination nous représente, à la pensée de n’importe quel objet spatial vu fréquemment, une image de celui-ci ; il est aussi utile et commode, pour juger plus aisément de l’objet, que nous ayons cette image dans la tête ; mais je ne le tiens pas pour absolument nécessaire à ce jugement. C’est ainsi en effet qu’il y a bien en géométrie des théorèmes pour lesquels nous n’avons aucune espèce d’intuition. La proposition selon laquelle toute ligne droite se peut prolonger à l'infini n'a aucune intuition pour elle ; les lignes que notre imagination peut représenter en nous ne sont pas infiniment longues »5.
La ligne droite ou le triangle sont, pour Bolzano, des concepts caractérisés par un ensemble de traits définitoires que ne satisfait peut-être aucune figure réelle donnée dans la perception sensible ni même d’ailleurs aucune figure imaginable. Et leurs propriétés, qu’énoncent les théorèmes géométriques, ne sont que les conséquences de leurs traits définitoires et non le résultat d’expériences visuelles, même purifiées :
- Note de bas de page 6 :
-
Bernard Bolzano, Contribution à une exposition mieux fondée des mathématiques, ibidem, § 7, p. 9.
« Kant semble vouloir dire : ‘Si je lie à une intuition le concept universel, par exemple d'un point ou d’une direction ou d'une distance, c’est-à-dire si je me représente un point singulier, une direction ou une distance singulières, alors je découvre dans ces objets singuliers que leur revient tel ou tel prédicat, et je sens en même temps que ceci vaut de même pour tous les autres objets qui tombent sous ce concept.’ Si tel est ce que veulent dire Kant et ses disciples, je pose la question suivante : comment en venons-nous donc, lors de l’intuition de tel objet singulier, au sentiment que ce que nous remarquons en lui, vaut aussi pour tout autre ? Au moyen de ce qui est singulier et individuel ; ou au moyen de ce qui est universel en cet objet ? A l’évidence seulement au moyen de ce qui est universel, c’est-à-dire au moyen du concept, non pas au moyen de l’intuition »6.
- Note de bas de page 7 :
-
Bernard Bolzano, Wissenschaftslehre, Leipzig, Felix Meiner, 1929, IV, § 394, tome II, pp. 15-23.
Contre l’idée kantienne selon laquelle les raisonnements mathématiques seraient fondés dans des intuitions pures, Bolzano insiste au contraire sur le caractère purement déductif de ces sciences conceptuelles pures que sont les mathématiques. Que ce soit à la logique qu’il revienne de fonder les preuves mathématiques, c’est ce que soutient Bolzano à partir du modèle des axiomatiques grecques7, lesquelles ont l’énorme mérite de mettre en évidence les vérités fondamentales caractérisant le sens des concepts centraux d’une science et de présenter rigoureusement les liens de conséquence qui rapportent à elles toutes les autres vérités du domaine.
Or, cette conception déductiviste des mathématiques sera nettement renforcée dans le courant du XIXème siècle par une série de développements géométriques autant qu’arithmétiques. Ainsi en va-t-il de manière particulièrement spectaculaire des géométries non-euclidiennes de Lobatchevski, Bolyai ou Riemann, qui montrent l’indépendance logique du cinquième postulat d’Euclide par rapport aux autres postulats du système euclidien, et la possibilité de le remplacer par des postulats alternatifs sans introduire aucune contradiction logique dans le système. De ces nouveaux systèmes se déduisent alors des jugements qui vont directement à l’encontre des évidences intuitives dont se réclamait Kant ; par exemple, la somme des angles du triangle devient inférieure à 180° dans la géométrie hyperbolique et supérieure à 180° dans la géométrie elliptique. Mais, en modifiant d’autres axiomes, sont aussi développés toute une série d’autres systèmes géométriques (géométrie affine, projective, non-archimédienne, ...) caractérisés par d’autres propriétés formelles. Parallèlement, les ensembles de nombres – entiers, rationnels, réels, complexes, mais aussi quaternions, etc. – font, en arithmétique, l’objet d’investigations systématiques, qui s’intéressent à leurs propriétés formelles indépendamment de leur caractère plus ou moins intuitif.
A la fin du XIXème siècle, Georg Cantor, dont l’étude de la notion d’infini témoigne nettement de la suprématie des considérations logiques sur les considérations intuitives, défend à cet égard un point de vue particulièrement tranché :
- Note de bas de page 8 :
-
Georg Cantor, « Fondements d'une théorie générale des ensembles », trad. partielle dans Cahiers pour l'Analyse, 1969, vol. 10, p. 48.
« La mathématique est pleinement libre dans son développement et ne connaît qu’une seule obligation [...] : ses concepts doivent être non contradictoires en eux-mêmes et soutenir d’autre part avec les concepts formés antérieurement, déjà présents et assurés, des relations fixes, réglées par des définitions. En particulier, pour pouvoir introduire de nouveaux nombres, il est seulement requis d’en donner des définitions leur conférant une précision et, le cas échéant, une relation aux anciens nombres telle que l’on puisse dans des cas donnés les distinguer des autres de manière déterminée. Dès qu’un nombre satisfait à toutes ces conditions, il peut et doit être considéré comme existant et réel dans la mathématique. Je vois dans ce fait la raison […] pour laquelle on doit accorder aux nombres rationnels, irrationnels et complexes tout autant d’existence qu’aux nombres entiers positifs finis »8.
L’idéographie au service de la déduction
- Note de bas de page 9 :
-
Gottlob Frege, Lois fondamentales de l'arithmétique, préfacetraduite dans J.P. Belna, La notion de nombre chez Dedekind, Cantor, Frege, Paris, Vrin, Mathesis, 1996, p. 341.
Que les mathématiques soient essentiellement déductives et non intuitives, fondées sur la non-contradiction plutôt que sur la figurativité visuelle, c’est ce qui justifie la mise au point de langages formels permettant de mettre en évidence la forme logique des énoncés mathématiques ainsi que les transformations que cette forme subit au cours des preuves, transformations dont on peut vérifier avec précision la conformité à un ensemble de règles d’inférence admises au départ. Ainsi rendues parfaitement rigoureuses et incontestables, les démonstrations mathématiques seraient alors libérées de tout recours à l’intuition – notamment à l’intuition de figures géométriques ou de représentations visuelles de nombres –, recours à l’évidence suspect de dissimuler bien des imprécisions et surtout bien des hypothèses inaperçues9.
- Note de bas de page 10 :
-
Gottlob Frege, Idéographie, Paris, Vrin, 1999,préface, pp. 6-7.
- Note de bas de page 11 :
-
Giuseppe Peano, Formulaire de mathématiques, Tome I, Turin, Bocca Frères et Ch. Clausen, 1895, pp. III-VI.
Dès 1879, Gottlob Frege formule le projet d’expliciter complètement les raisonnements mathématiques dans une « idéo-graphie » ou « écriture conceptuelle » (Begriffsschrift) de manière à en « examiner de la manière la plus sûre la force concluante »10. A la même époque, Giuseppe Peano se lance lui aussi dans un ambitieux projet de formalisation des mathématiques, dont les principes fondateurs affichent les mêmes objectifs de mise en évidence univoque et précise des structures logiques de leurs jugements et raisonnements11. De même, Charles Sanders Peirce s’efforce de mettre au point un langage formel qui reflèterait dans sa syntaxe les articulations logiques de la pensée et exhiberait par là même le rôle de ces articulations au sein des raisonnements.
Outre leurs vertus de clarification et d’expression rigoureuse de la pensée, de telles notations symboliques comportent d’indéniables avantages opératoires. A cet égard, les fondateurs de la logique symbolique – au rang desquels il faudra aussi compter Bertrand Russell et Alfred North Whitehead, qui donneront à la logique contemporaine une langue canonique inspirée de celles de Frege et de Peano – renouent explicitement avec le projet leibnizien d’une lingua characteristica qui se fait aussi calculus ratiocinatior. En calquant ses structures syntaxiques sur les structures logiques de la pensée, la langue formelle permet un travail de transformations inférentielles qui opère sur les symboles eux-mêmes et s’apparente à un simple calcul. Comme le dit Peano :
- Note de bas de page 12 :
-
Giuseppe Peano, Formulaire de mathématiques, Tome III, op. cit., pp. III-IV. « C'est, dit aussi Frege, précisément dans la possibilité d'exécuter une sorte de calcul que Leibniz voyait un avantage principal d'une écriture qui compose le concept à partir de ses constituants » (Gottlob Frege, « La logique calculatoire de Boole et l'idéographie », Ecrits posthumes, Nîmes, Jacqueline Chambon, 1994, p. 17).
« Le but des recherches de Leibniz était de créer une sorte de Spécieuse Générale, où toutes les vérités de raison seraient réduites à une façon de calcul. Ce pourrait être en mêmes temps une manière de Langue ou d’Ecriture universelle, mais infiniment différente de toutes celles qu’on a projetées jusqu’ici; car les caractères y dirigeraient la Raison ; et les erreurs excepté celles de fait, n’y seraient que des erreurs de calcul »12.
Comme c’est le cas en algèbre, chaque formule n’est qu’une transformation de la précédente conformément à un ensemble de règles simples et préalablement données, de sorte que le raisonnement formalisé peut faire l’objet d’un contrôle minutieux pas à pas et qu’est évacué tout recours à l’appréciation subjective de la plus ou moins grande « évidence » de chaque inférence. Reste que, comme vont bientôt le faire apparaître les théoriciens de la démonstration, ces preuves formelles tirent elles-mêmes leur pouvoir de conviction d’une certaine évidence visuelle de leurs transformations symboliques.
L’idéographie au service de l’intuition
Peirce lui-même y insiste d’emblée ; démontrer, c’est montrer. Parce qu’elle exhibe un certain nombre de rapports logiques, la preuve formelle revêt des traits résolument diagrammatiques et non pas seulement symboliques :
- Note de bas de page 13 :
-
Charles Sanders Peirce, « Sur l’algèbre de la logique. Une contribution à la philosophie de la notation », Œuvres III. Ecrits logiques, Paris, Cerf, 2006, pp. 281-282. Cf. aussi Charles Sanders Peirce, « Principes d’interprétation », p. 336 : « Notre but est d’étudier les opérations de l’inférence nécessaire. Afin de le réaliser, ce que nous voulons, c’est une méthode de représentation diagrammatique de tout ensemble possible de prémisses, ce diagramme devant être tel que nous puissions observer la transformation de ces prémisses en conclusion par une série d’étapes dont chacune soit de la plus extrême simplicité possible ».
« Tout raisonnement déductif, même le simple syllogisme, implique un élément d’observation ; à savoir que la déduction consiste à construire une icône ou diagramme dont les relations des parties doivent présenter une complète analogie avec celles des parties de l’objet du raisonnement, à expérimenter sur cette image dans l’imagination et à observer le résultat de façon à découvrir des relations entre les parties qu’on n’avait pas remarquées et qui restaient cachées »13.
- Note de bas de page 14 :
-
David Hilbert, « Lettre à Frege du 29 décembre 1899 », Logique et fondements des mathématiques, Paris, Payot, 1992, p. 227.
- Note de bas de page 15 :
-
« Si les axiomes arbitrairement posés avec toutes leurs conséquences ne se contredisent pas, dit Hilbert, alors ils sont vrais et les choses qu’ils définissent existent. C'est pour moi le critère de la vérité et de l'existence » (David Hilbert, « Lettre à Frege du 29 décembre 1899 », ibidem, p. 227).
Peirce, cependant, n’est pas le seul à formuler ce constat. David Hilbert, maître à penser de l’école formaliste, est un de ceux qui ont poussé le plus loin le rejet de l’intuition en mathématiques au profit de la seule déduction formelle. Ainsi, dans ses Fondements de la géométrie, il a établi la géométrie comme un pur système déductif qui ne repose en rien sur quelque précompréhension intuitive initiale des notions de « point », de « droite » et de « plan », mais définit intrinsèquement ces concepts au sein du système, de sorte que, par exemple, « en géométrie euclidienne, non euclidienne, archimédienne, non archimédienne, ‘point’ est à chaque fois quelque chose de différent »14. Comme Cantor, Hilbert voit dans l’exigence logique de non-contradiction le critère ultime de la vérité des énoncés mathématiques15 ; et, à cet égard, il s’oppose explicitement aux mathématiciens de son temps (comme Leopold Kronecker, Henri Poincaré, Emile Borel, ou Luitzen Egbertus Brouwer) qui persistent à penser que l’intuition et la construction intuitive jouent un rôle fondamental, non seulement dans la découverte des thèses mathématiques, mais aussi dans leur justification.
Pourtant, alors même qu’il soutient que la déduction doit entièrement remplacer l’intuition dans le raisonnement mathématique, Hilbert reconnaît comme Peirce que, dans sa présentation même, la preuve formelle comporte une dimension inéluctablement figurative. Bien qu’elle consiste désormais entièrement en un calcul, c’est-à-dire en un ensemble de transformations réglées opérant sur les formules symboliques elles-mêmes et sans plus de référence à leur contenu, la démonstration mathématique suppose cependant que ces transformations symboliques elles-mêmes jouissent d’une certaine « évidence ». Car ce sont en fait les symboles qui sont devenus le contenu intuitif du raisonnement :
- Note de bas de page 16 :
-
David Hilbert, « Nouvelle fondation des mathématiques », Intuitionisme et théorie de la démonstration, Paris, Vrin, Mathesis, 1992, p. 119.
« Les axiomes, formules et démonstrations en quoi consiste l’édifice formel, sont exactement ce qu’étaient les chiffres dans la construction [...] de l’arithmétique élémentaire, et ce sont eux qui deviennent maintenant, tels les chiffres en arithmétique, le thème de raisonnements contentuels, i.e. de la pensée véritable »16.
- Note de bas de page 17 :
-
David Hilbert, « Nouvelle fondation des mathématiques », ibidem, p. 123.
- Note de bas de page 18 :
-
Sur la notion de « transformations géométriques », cf. notamment Groupe µ, Traité du signe visuel, Paris, Le Seuil, 1992, pp. 158-163.
Une preuve formelle, dit Hilbert, « est un dessin qui doit se présenter devant nous comme tel dans l’intuition sensible »17. Là où, pour prouver un théorème sur la somme des angles du triangle, le géomètre s’appuyait sur l’observation de la figure dessinée d’un triangle et des transformations visuelles qu’il lui pouvait lui faire subir, il s’appuie désormais sur l’observation de certaines configurations spatiales de symboles dans des formules et sur les « transformations géométriques » (transformations, permutations, congruences, …)18 qu’elles subissent sur le papier de la démonstration. Et c’est là une thèse que l’on retrouve presque à l’identique chez Ludwig Wittgenstein :
- Note de bas de page 19 :
-
Ludwig Wittgenstein, Remarks on the foundations of mathematics, Oxford, Basil Blackwell, 3rd edition, 1978, § III-43, pp. 174-175.
« La puissance démonstrative de la preuve logique coïncide et se confond avec sa puissance démonstrative géométrique [qui a trait à la transformation visuelle des symboles]. Cela signifie : la preuve logique de type russellien n’a de puissance démonstrative que dans la mesure où elle possède également une puissance persuasive géométrique »19.
- Note de bas de page 20 :
-
Sur la notion de « toposyntaxe », cf. Jean-Marie Klinkenberg, « A quoi servent les schémas ? Tabularité et dynamisme littéraire », Protée, vol. 37, n°3, 2009, pp. 66.
On le voit ; de l’aveu même des théoriciens de la démonstration qui ont le plus insisté sur sa nature logico-déductive, il y a une part indépassablement figurative – ou « toposyntaxique »20 – dans la preuve formelle, dimension qui requiert les investigations de la sémiotique visuelle. Il ne faudrait pas, toutefois, croire qu’on en revient alors à l’ancien recours à l’évidence et qu’« il n’y a qu’à voir » la validité de l’inférence. Montrer, en effet, c’est aussi mettre en évidence et cela suppose tout un ensemble de procédés de présentation formelle visant à construire l’évidence de la démonstration, procédés qu’on n’hésitera pas à qualifier de « rhétoriques ».
Faire voir
- Note de bas de page 21 :
-
Chaïm Perelman et Lucie Olbrechts-Tyteca, « Logique et rhétorique », Revue philosophique de la France et de l’étranger, Paris, janvier-mars 1950, reproduit dans Rhétoriques, Editions de l’Université de Bruxelles, 1989, p. 64.
- Note de bas de page 22 :
-
« Le recours à l’évidence donnait au rationalisme classique une assurance que le rationalisme rhétorique ne possède plus, car ce qui pour celui-là se présentait comme une certitude ne peut constituer pour celui-ci qu’une hypothèse soumise à l’épreuve; il ne suffit plus de présumer l’accord de l’auditoire universel, il faut s’en assurer effectivement » (Chaïm Perelman, « Rhétorique et philosophie », Les études philosophiques, Paris, 1969, reproduit dans Rhétoriques, op. cit., p. 217).
Dans leur Traité de l’argumentation, Chaïm Perelman et Lucie Olbrechts-Tyteca ont souligné la naïveté non critique du recours à l’évidence comme moyen de preuve21. Bien sûr, il ne s’agit pas, pour les tenants de la « nouvelle rhétorique », de contester que la conviction rationnelle repose en dernière analyse sur un certain nombre d’évidences, mais bien que ces évidences soient entièrement naturelles et indépendantes de toute construction. La thèse rhétorique, c’est justement que ces évidences sont construites dans l’argumentation22.
- Note de bas de page 23 :
-
« Ce qui nous convainc, c’est ça la preuve. Une configuration qui ne nous convainc pas n’est pas la preuve » (Ludwig Wittgenstein, Remarks on the foundations of mathematics, ibidem, § III-39, p. 171).
- Note de bas de page 24 :
-
Ludwig Wittgenstein, Cours sur les fondements des mathématiques, Mauvezin, T.E.R., 1995, cours VII,
p. 63.
Qu’une preuve ne puisse se réduire à la pure et simple exhibition de rapports logiques dans des configurations spatiales et qu’il y ait une dimension proprement rhétorique dans la présentation des preuves formelles, c’est d’ailleurs ce qu’avait aussi dit Wittgenstein23. La raison en est, selon ce dernier, qu’un schéma ne peut fournir lui-même les principes de son interprétation. L’image qui relie par des traits les sommets d’un pentacle aux doigts d’une main24 est-elle une preuve de leur équinuméricité ? Ne peut-on produire une image qui relierait de la même manière des points quelconques de figures quelconques ? Le problème soulevé ici par Wittgenstein est celui de l’incapacité d’une figure à énoncer elle-même ce qu’elle montre. Dans une preuve formelle, les inférences logiques sont reflétées par certaines transformations géométriques opérées sur des formules symboliques. Mais la conformité des secondes aux premières n’est pas elle-même figurée dans la présentation visuelle de la preuve ; elle suppose une interprétation externe à celle-ci.
- Note de bas de page 25 :
-
« Notre paradoxe était celui-ci : une règle ne pourrait déterminer aucune manière d’agir, étant donné que toute manière d’agir peut être mise en accord avec la règle » (Ludwig Wittgenstein, Recherches philosophiques, Paris, Gallimard, 2004, § 201, p. 126).
- Note de bas de page 26 :
-
Ludwig Wittgenstein, Remarks on the foundations of mathematics, Oxford, Basil Blackwell, 3rd edition, 1978, § I-113, p. 79
Il ne faut pas, cependant, voir là une faiblesse propre à l’image et qui la subordonnerait irrémédiablement au langage verbal. La thèse wittgensteinienne s’étend en effet à ce dernier : aucune formulation de règle ne peut prescrire la manière dont elle doit être interprétée, de sorte qu’il est toujours théoriquement possible de juger une action conforme à la règle moyennant une certaine interprétation de celle-ci25. Et la chose est bien sûr également vraie de ces règles particulières que sont les lois logiques ; une démonstration peut certes se conformer à des règles d’inférence préalablement admises mais pas elle-même énoncer qu’elle s’y conforme26. Ce problème, sur lequel nous reviendrons, est en fait celui de la possibilité pour un langage d’être son propre métalangage et pour un discours d’être son propre métadiscours. Pour Wittgenstein, il y a là une impossibilité principielle, qui résulte de la distinction entre « dire » et « montrer ».
- Note de bas de page 27 :
-
« La proposition ne peut figurer (darstellen) la forme logique, elle en est le miroir. Ce qui se reflète dans la langue, celle-ci ne peut le figurer. Ce qui s’exprime dans la langue, nous ne pouvons par elle l’exprimer. La proposition montre la forme logique de la réalité. Elle l’indique » (Ludwig Wittgenstein, Tractatus logico-philosophicus, Paris, Gallimard, 1993, § 4.121, p. 58).
- Note de bas de page 28 :
-
Ludwig Wittgenstein, Tractatus logico-philosophicus, ibidem, § 2.13, 2.14, 2.15, 2.17, 2.171, 2.172, pp. 38-39.
- Note de bas de page 29 :
-
Ludwig Wittgenstein, Tractatus logico-philosophicus, ibidem, § 4.0312, 4.04, 4.041, pp. 54-55. A noter que, comme l’indique d’ailleurs le modèle du tableau, cette « iconicité » du langage formel à l’égard de la pensée rationnelle est moins copie que reconstruction (cf. sur ce point la critique de l’iconicité dans GROUPE µ, Traité du signe visuel, ibidem, pp. 124-127).
Le Tractatus logico-philosophicus avait en effet insisté sur le fait que l’idéographie peut exhiber la forme logique de la pensée rationnelle, mais pas proprement la figurer ou la dire27. Par la disposition spatiale de ses tâches de couleur, un tableau peut représenter un paysage de même forme. Mais, contrairement à tel ou tel élément du paysage – tel nuage, tel arbre au feuillage sombre –, la forme d’ensemble n’est elle-même nulle part dépeinte dans le tableau ; le tableau ne figure pas la forme du paysage mais la reflète dans sa propre forme28. Or, il en va exactement de même du rapport du langage formel au contenu pensé à travers lui. Le langage formel « reflète », « exhibe », « montre » par sa propre forme la forme logique des contenus pensés, mais il ne prend pas cette forme elle-même pour contenu ; il ne la « dit » et ne la « figure » pas29.
- Note de bas de page 30 :
-
« Que la vérité d’une proposition suive de la vérité d’autres propositions, nous le voyons par leur structure. Si la vérité d’une proposition suit de la vérité d’autres propositions, ceci s’exprime dans les relations qu’ont entre elles leurs formes » (Ludwig Wittgenstein, Tractatus logico-philosophicus, ibidem, § 5.131, 5.1311, pp. 72-73).
Dans une preuve formelle, les articulations logiques sont reflétées par la configuration d’ensemble, mais elles ne sont elles-mêmes figurées nulle part, même pas vraiment dans les symboles des connecteurs logiques. C’est dans la structure des formules et non dans l’un de leurs éléments que se manifestent leurs propriétés et relations logiques30. Peirce, déjà, faisait bien comprendre pourquoi c’est le cas. On pourrait croire qu’il est toujours possible de dire, à titre de prémisse supplémentaire, le principe d’inférence qui permet de passer des prémisses à la conclusion du raisonnement. Ainsi, pour déduire la conclusion « La route est mouillée » des prémisses « S’il pleut, alors la route est mouillée » et « Il pleut », je pourrais peut-être ajouter la prémisse « Quant l’antécédent d’un conditionnel est réalisé, s’en suit la réalisation du conséquent », qui explicite le principe d’inférence du Modus Ponens et ne laisse ainsi plus rien d’implicite dans l’inférence. Mais c’est là un leurre, car le principe qui permet d’inférer la conclusion de ces trois prémisses resterait à son tour inexplicité :
- Note de bas de page 31 :
-
Charles Sanders Peirce, « Sur la classification naturelle des arguments », Œuvres III. Ecrits logiques, op. cit., p. 56.
« On peut montrer qu’il y a des arguments dont aucune partie du principe directeur ne peut être transférée aux prémisses (…). Car, soit les prémisses d’un argument désignées par P, la conclusion par C, et le principe directeur par L. Alors, si la totalité du principe directeur est exprimée comme prémisse, l’argument devient
L et P
\ C
Mais ce nouvel argument doit aussi avoir son principe directeur, qui peut être désigné par L’. (…) D’où tout argument a, comme partie de son principe directeur, un certain principe qui ne peut être éliminé de son principe directeur. Un tel principe peut être appelé principe logique »31.
- Note de bas de page 32 :
-
Sur les rapports entre les deux sens du mot « rhétorique », cf. Bruno Leclercq, « Néo-rhétoriques ‘made in Belgium’ : figures de style et argumentation », à paraître dans la revue Argumentum.
On comprend donc tout à la fois pourquoi démontrer, c’est montrer – exhiber des rapports logiques dans des configurations spatiales – et pourquoi montrer ne suffit pas à démontrer – il faut encore convaincre que ce qu’on voit là sont bien des rapports logiques. D’où l’importance d’une analyse sémiotique et rhétorique du (dé)montrer, d’une étude des procédés du « faire voir » et du « mettre en évidence ». Dans la mesure où il s’agit de procédés figuratifs producteurs d’effets de conviction sur tel ou tel auditoire, le terme « rhétorique » semble ici tout à fait légitime dans le sens qu’a privilégié Perelman. C’est toutefois dans les travaux du Groupe µ que nous trouverons les indications les plus précieuses pour aborder cette question des procédés « rhétoriques »32 qui sous-tendent la figurativité et le pouvoir (dé)monstratif des preuves formelles. Nous nous bornerons à suggérer ici trois dimensions de cette problématique.
Narration et petits pas
- Note de bas de page 33 :
-
Groupe µ, Traité du signe visuel, ibidem, pp. 210-221.
- Note de bas de page 34 :
-
Groupe µ, Traité du signe visuel, ibidem, p. 328.
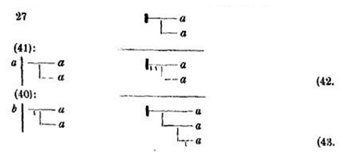
Un premier enjeu consiste bien sûr dans la nécessité d’introduire dans l’image des facteurs d’orientation lui permettant de représenter un développement « linéaire » comme l’est une démonstration. Dans son Traité du signe visuel, le Groupe µ a mis en évidence certains procédés figuratifs qui permettent de linéariser une image et de lui conférer une dimension chronologique voire même narrative33. Ainsi, dans la figure (17b) de la transformation progressive d’un carré en cercle34, c’est l’alignement ordonné des figures, ainsi que le cumul des transformations visuelles, qui fournissent à l’image sa direction d’ensemble :
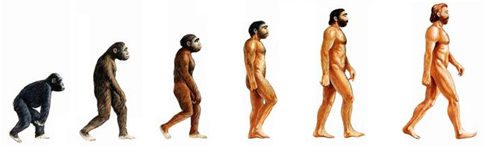
Dans des images similaires, comme la célèbre « marche du progrès », cette directionalité (réversible) se voit en outre imposer un sens univoque gauche-droite du fait de l’orientation même des différents éléments de la suite (les ancêtres de l’homme), qui se dirigent clairement vers la droite :
C’est d’ailleurs sur ce trait sémiotique du « sens de la marche » que joue la transformation, cette fois proprement rhétorique au sens du Groupe µ, qui préside à la construction de l’image humoristique suivante :
- Note de bas de page 35 :
-
Groupe µ, Traité du signe visuel, ibidem, pp. 214-215.
Dans l’image originaire, la « progression » gauche-droite est en outre renforcée, dans sa dimension axiologique, par l’accroissement de la taille des éléments, formème sémiotique35 qui permet à son tour des variations « rhétoriques », qui le soulignent a contrario :
- Note de bas de page 36 :
-
Sur ce point, cf. notamment les analyses du Groupe µ, « L’effet de temporalité dans les images fixes », in Texte, n° 21-22, 1997, p. 63, et Jean-Marie Klinkenberg, « A quoi servent les schémas ? Tabularité et dynamisme linéaire », Protée, vol. 37, n°3, pp. 67-68.
Un autre facteur du formème « orientation », cependant, est aussi imposé à l’image de l’extérieur et par l’interférence de la syntaxe d’un autre code, celui de l’écriture linguistique36. Il est en effet clair que le choix du sens gauche-droite pour marquer la progression (chronologique et axiologique) n’est pas totalement fortuit.
Or, il y a là un nouvel élément intéressant pour l’analyse sémiotique et rhétorique de la preuve formelle en tant qu’image. Car, si l’orientation de l’image semble un trait essentiel à sa capacité même de figurer un développement tel qu’une démonstration, il semble qu’un avantage persuasif (ou « rhétorique » au sens de Perelman) aille plus particulièrement aux orientations gauche-droite et haut-bas du fait de leur conformité à la norme du développement linguistique. Or, cela est évidemment d’autant plus vrai pour la preuve formelle, dans la mesure où celle-ci n’est pas seulement un calcul fait de règles de transformation entre formules prises comme configurations spatiales de symboles, mais aussi langage, dont on s’attend donc à ce qu’il présente certains traits du langage naturel qu’il formalise. Nous reviendrons plus loin sur cette « intersémioticité » de la preuve formelle.
- Note de bas de page 37 :
-
Charles Sanders Peirce, « Principes d’interprétation », Œuvres III. Ecrits logiques, ibidem, p. 336.
Avant cela, soulignons encore que, comme le mouvement des primates figurés dans la « marche du progrès », le développement démonstratif doit « marcher d’un bon pas », c’est-à-dire qu’il doit se décomposer en une série de pas qui ne soient ni trop nombreux – pour qu’on puisse saisir d’un seul coup d’œil l’ensemble du processus – ni trop peu nombreux – pour que la transformation préserve suffisamment d’invariant (et reste plausible) à chaque étape –, mais aussi en une série de pas qui soient suffisamment réguliers pour ne pas laisser paraître la possibilité de « chaînons manquants » dans un processus qui se doit d’être ininterrompu. A cet égard, une stratégie que développent les logiciens et mathématiciens lorsque, de fait, la preuve est longue et irrégulière (au sens où elle sollicite des moyens démonstratifs d’ordres différents) consiste à décomposer cette preuve en plusieurs composantes – parfois explicitement détachées comme « lemmes » – qui bénéficient chacune séparément d’une certaine évidence globale et peuvent par ailleurs être rassemblées dans une présentation synthétique de la preuve complète dont l’évidence est elle-même globalement « supervisable ». Mais, à l’inverse, donc, chaque étape doit être explicitée : comme y insiste Peirce, « le diagramme doit être tel que nous puissions observer la transformation des prémisses en conclusion par une série d’étapes dont chacune soit de la plus extrême simplicité possible »37. Et, sous peine de tout remettre en cause, est évidemment exclu le moindre chaînon manquant, le moindre saut entre deux étapes du développement qui ne soit pas « assuré » par un principe d’inférence admis au départ.
Indications métalinguistiques
On parvient là à un second enjeu qui mérite de plus longues investigations. Généralement, en effet, la suite de formules qui compose une preuve formelle s’accompagne, en marge, d’un ensemble d’indications sur les règles d’inférence qui justifient le passage d’une formule à l’autre, la transformation de l’une dans l’autre. Dans la mesure où la preuve prétend ne reposer que sur des principes déductifs préalablement admis, ces indications sont évidemment essentielles au pouvoir démonstratif – et à la force persuasive – de la preuve.
- Note de bas de page 38 :
-
Alfred Tarski, « The concept of truth in formalized languages of the deductive sciences », Logic, Semantics and Metamathematics. Papers from 1923 to 1938, Indianapolis, Hackett, 1983, pp. 152-278 ; Alfred Tarski, « The semantic conception of truth », Philosophy and Phenomenological Research, vol. 4, 1944, pp. 13–47. Rudolf Carnap, Die logische Syntax der Sprache, Vienne, Julius Springer, 1934 ;Rudolf Carnap, Introduction to semantics, Cambridge Mass., Harvard University Press, 1942.
Se pose alors la question du statut sémiotique de ces indications. S’agit-il de « légendes », c’est-à-dire de commentaires linguistiques extérieurs à l’image – bien qu’éventuellement insérés artificiellement en elle – qui précisent ce que l’image montre et comment il faut l’interpréter ? Cela confirmerait tout à la fois la thèse wittgensteinienne selon laquelle une idéographie ne peut pas dire ce qu’elle montre – c’est-à-dire qu’elle ne peut ni directement énoncer les formes qu’elle exhibe ni même indiquer qu’elle a pour fonction de les exhiber – et la réponse que lui ont rapidement adressée des logiciens comme Alfred Tarski ou Rudolf Carnap, à savoir que la forme d’un langage formel ne peut certes pas nécessairement être énoncée en lui, mais qu’elle peut l’être dans un autre langage qui se comporte à son égard comme un métalangage38.
- Note de bas de page 39 :
-
C’est en particulier le statut sémiotique des « invariantes génératrices », expressions générales qui partagent la forme de leurs instanciations particulières et se prêtent donc aux mêmes opérations formelles que ces dernières, qu’Alain Herreman étudie dans « Vers une analyse sémiotique de la théorie des ensembles : Hiérarchies et réflexivité », Philosophia scientiae, vol. 9, n° 2, 2005, pp. 165-187. Cf. aussi Alain Herreman, « Remarques générales sur l’expression de la généralité en mathématiques », Texto ! [En ligne], 2010, URL : http://www.revue-texto.net/index.php?id=2513. Merci à Sémir Badir d’avoir attiré notre attention sur ces travaux.
Incontestablement, les indications marginales d’une preuve formelle sur les principes logiques qui régissent les transformations visuelles opérées sur ses formules à chaque étape ont un caractère métalinguistique. Le fait que ces indications soient souvent formulées dans la langue naturelle semblerait alors conforter la thèse de certains sémioticiens selon laquelle les images ne peuvent rien démontrer sans s’insérer dans des textes où elles trouvent l’indispensable support d’énoncés proprement linguistiques. Il se fait cependant que, en vertu de traits de « réflexivité » propres aux langages formels qu’a bien mis en évidence Alain Herreman39, les indications « métalinguistiques » qui figurent des preuves peuvent tout aussi bien se présenter sous forme de configurations parfaitement analogues à celles du « langage-objet » qu’elles commentent.
- Note de bas de page 40 :
-
Ainsi, la formule justificative doit figurer sur la même ligne que la formule de la preuve qui est obtenue conformément à elle ou alors sur une ligne intermédiaire entre cette formule et la formule précédente. Sur la syntaxe de juxtaposition, cf. le Traité du signe visuel (op. cit., pp. 213-214) pour les questions de centralité et de marginalité, mais aussi « L’effet de temporalité dans les images fixes », ibidem, pp. 51-52 pour les facteurs de proximité et de couplage.
La distinction entre langage et métalangage est en fait moins nette qu’il paraît. Lorsqu’ils ont montré qu’on pouvait sortir d’un langage pour en étudier les formes dans un métalangage, Tarski et Carnap ont aussi établi que ce métalangage pouvait n’être autre que le premier langage simplement enrichi d’un peu de pouvoir expressif supplémentaire. Dans le cas des preuves formelles, cela implique que les indications métalinguistiques peuvent à leur tour revêtir une présentation essentiellement figurative, qui s’insère alors dans l’image d’une manière d’autant moins artificielle que la similarité perceptible des configurations entre formules du langage-objet et formules du métalangage constitue le fondement même de la justification que les secondes fournissent aux premières. Certes, la distinction entre langage-objet et métalangage n’en est-elle pas pour autant totalement abolie, mais il semble ici qu’elle reste interne à la sémiotique visuelle, puisque c’est à une image que revient la tâche de commenter l’image qui lui est juxtaposée. Bien plus, la juxtaposition même de ces deux images au sein d’une seule et même troisième qui constitue la preuve proprement dite répond à des principes de configuration spatiale qui relèvent une fois encore de la sémiotique et de la rhétorique visuelles. Peut-être même la richesse d’expression supplémentaire que requiert le métalangage pour commenter le langage-objet tient-elle exclusivement à ces règles de juxtaposition entre formule du langage et du métalangage40.
- Note de bas de page 41 :
-
La même chose vaut bien entendu de l’introduction, dans l’image, de signes d’« assertion » (comme le symbole du « turnstile », qui précède chaque ligne de la preuve chez Russell comme chez Frege). Un autre cas encore est celui des indications C.Q.F.D. (ou Q.E.D.), qui exercent quant à elles une fonction de « bordure » (Groupe µ, Traité du signe visuel, ibidem pp. 378-381).
Voilà qui indiquerait alors qu’une image peut bien démontrer seule, et ce notamment parce que, contrairement à ce que dit Wittgenstein, elle peut s’adjoindre des éléments métalinguistiques qui sont eux-mêmes figuratifs et lui permettent ainsi de montrer ce qu’elle montre. Reste, cependant, et tel est l’acquis de Wittgenstein comme déjà de Peirce, que vouloir régler le problème de l’interprétation de l’image en introduisant en elle des éléments figuratifs métalinguistiques41 ne peut que mener à une régression à l’infini, puisque l’image totale – dérivation formelle + justifications formelles – doit elle-même encore être interprétée. Peut-être les figures métalinguistiques montrent-elles le sens et la validité des transformations visuelles entre formules de la dérivation ; mais qu’est-ce qui, dans l’image, montre qu’elles le font ? En principe, leur présence aux côtés des transformations formelles doit légitimer ces dernières en mettant en évidence qu’elles leur sont conformes. Mais qu’est-ce qui, à son tour, montre que c’est là leur rôle et qu’est-ce qui atteste de cette « conformité » ? Comme l’indiquait Peirce, le principe logique qui fonde l’inférence du raisonnement ne peut être explicité dans le raisonnement sans qu’il revienne à charge d’un autre principe logique de fonder l’inférence entre l’ensemble des prémisses ainsi enrichi et la conclusion. Et c’est pourquoi aussi Wittgenstein soutenait qu’énoncer une règle ne suffit pas à justifier un acte, puisqu’il convient encore de rendre compte par une autre règle (qui interprète la première) de la conformité de l’acte à la règle.
Démontrer ne se réduit donc jamais à montrer ; même complexe, une image seule ne démontre pas. Mais, pour autant, démontrer est-ce alors dire ? En revient-on à la thèse de la nécessité de sortir de l’image et de l’accompagner d’un commentaire linguistique verbal qui interrompt la régression à l’infini des monstrations en disant une fois pour toutes ce qui est montré ? Non. La thèse de Peirce et Wittgenstein est générale est elle vaut aussi de ce qui est dit. On peut donc en principe toujours s’interroger sur la conformité de l’image à ce qu’en dit la légende et puis de cette légende à ce qu’en dit tel ou tel paragraphe du texte dans lequel l’image s’insère, et ainsi de suite… Le problème que soulèvent Peirce et Wittgenstein ne condamne pas seulement la pleine capacité démonstrative des images mais tout aussi bien celle des énoncés ou même des développements linguistiques. Aucun énoncé linguistique ou figural ne contient en lui-même de manière explicite les principes qui en font une démonstration. A cet égard, même si elle pâtit peut-être, par rapport au langage verbal, de handicaps spécifiques qu’il conviendrait à une sémiotique comparative de dévoiler, la figuration ne souffre pas nécessairement, dans sa capacité démonstrative, d’un défaut de nature plus grave que le langage verbal.
Notations et lisibilité
- Note de bas de page 42 :
-
Bertrand Russell, Principes des mathématiques, appendice A, traduction française partielle dans Ecrits de logique philosophique, Paris, Presses Universitaires de France, coll. Epiméthée, 1989, p. 159. Cf. aussi Bertrand Russell et Alfred North Whitehead, Principia mathematica, chap. I, traduction française partielle dans Ecrits de logique philosophique, ibidem, p. 225.
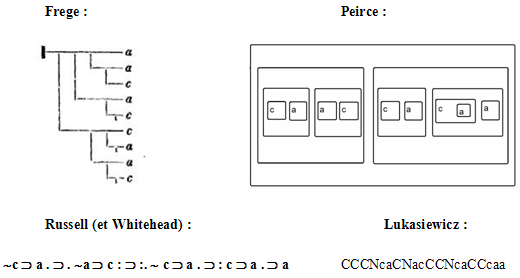
Un troisième et dernier enjeu de l’efficacité rhétorique des preuves formelles réside dans le choix de conventions de notation et de présentation. Bien que Bertrand Russell estimât l’idéographie frégéenne « fondée sur une analyse des notions logiques beaucoup plus profonde que celle de Peano » et qu’il la jugeât « très supérieure d’un point de vue philosophique »42, c’est en définitive une notation « plus commode » d’inspiration péanienne qu’il privilégia lui-même et que toute la communauté scientifique fit sienne après lui. La raison principale de ce choix réside sans doute dans le fait que l’écriture bidimensionnelle de Frege, qui satisfaisait par ailleurs toutes les exigences du calcul, combinait par contre le double désavantage de se démarquer par trop des formes d’expression du langage quotidien, dont elle prétendait pourtant constituer une expression plus rigoureuse, et d’introduire en outre une certaine confusion visuelle entre l’expression des thèses et celle des liens de conséquence entre elles :
Formulée dans le langage « péanien » des Principia mathematica, la preuve (par ailleurs différente) du même théorème par Russell et Whitehead fait plus clairement apparaître la distinction entre les thèses, qui, comme les énoncés du langage quotidien, se présentent dans une linéarité horizontale, et leur enchaînement inférentiel qui se fait quant à lui sur l’axe vertical :
D’une manière plus générale, la question de l’efficacité persuasive d’un système notationnel pour les preuves formelles est évidemment directement liée aux problèmes de lisibilité, qui sont eux-mêmes fonction de facteurs naturels – comme la sensibilité de la perception visuelle à l’égard de certaines formes ou configurations (Gestalten) – et de facteurs plus culturels comme la similarité avec la syntaxe de codes déjà appris, en particulier de codes linguistiques. On peut, à ce double égard, contraster par exemple les notations respectivement expérimentées par Frege, Peirce, Russell et Lukasiewicz pour une seule et même forme logique :
Le principal avantage de la notation russellienne de cette formule est sans doute, nous l’avons suggéré, de présenter, par sa linéarité unidimensionnelle (contrairement aux notations frégéenne et peircienne) et par l’inscription des connecteurs logiques entre les propositions qu’ils relient (contrairement aux trois autres notations), une plus grande similarité visuelle avec l’énoncé de la langue naturelle qu’il est censé formaliser. Sa lisibilité en est d’autant renforcée pour tout qui est plus familier des structures syntaxiques du langage quotidien que de celles des algorithmes mathématiques. Les autres notations avaient par contre l’énorme avantage de mettre plus clairement en évidence la hiérarchie des connecteurs logiques de la formule, dont la notation russellienne s’efforce péniblement de rendre compte en indiçant les connecteurs d’un certain nombre de « points » qui témoignent de leur prévalence sur d’autres connecteurs dans chacune des deux directions. Un bon compromis entre ces deux avantages apparemment conflictuels réside sans doute dans le remplacement des points de Russell par un système hiérarchisé de parenthèses comme dans la notation suivante, qui est assez « standard » aujourd’hui :
- Note de bas de page 43 :
-
Cf. le principe « gestaltiste » de proximité, qui constitue un des ressorts de la sémiotique visuelle du Groupe µ (Traité du signe visuel, ibidem, pp. 34-37).
- Note de bas de page 44 :
-
La tabularité indique la multiplicité des axes sémiotiques. Tandis que la Rhétorique de la poésie (Bruxelles, Editions Complexe, 1977, pp. 115 et sq.) s’était intéressée à la tabularisation du langage verbal (normalement linéaire du fait de son lien au canal auditif), les travaux du Groupe µ en sémiotique visuelle se sont au contraire souvent attardés sur les processus de linéarisation (et notamment d’orientation temporelle) de l’image, notamment par la juxtaposition de formes. Cf. notamment « L’effet de temporalité dans les images fixes », ibidem, pp. 49-50 ou Jean-Marie Klinkenberg, « A quoi servent les schémas ? Tabularité et dynamisme linéaire », ibidem, pp. 69-70.
- Note de bas de page 45 :
-
Ce dont témoignent notamment une segmentation nette et un fort codage, qui manquent généralement à l’image (Groupe µ, Traité du signe visuel, ibidem, pp. 55-56, pp. 60-61).
Tout en respectant la linéarité du langage quotidien, le parenthésage met en évidence les articulations logiques en imposant des regroupements à la perception visuelle43. Et c’est clairement cette configuration spatiale résultant du parenthésage qui fait la supériorité de l’idéographie sur la langue quotidienne pour la conduite des raisonnements. Seule cette structuration figurative des thèses sur l’axe horizontal rend en effet possible leur articulation « tabulaire »44 avec la monstration verticale des transformations inférentielles. Mais c’est précisément pourquoi il est absolument nécessaire de considérer les preuves formelles en tant qu’images et d’en offrir des analyses de sémiotique et rhétorique visuelles plutôt que simplement linguistiques. C’est là tout ce que suggère Wittgenstein lorsqu’il prétend que l’idéographie « montre » des choses qu’elle ne « dit » pas. Certes, le langage symbolique est encore un langage45 – et nous venons d’ailleurs de montrer toute l’importance rhétorique à ce qu’il se présente en tant que tel –, mais il n’est pas qu’un langage car sa structure même est résolument figurative.